Yahtzee High Score

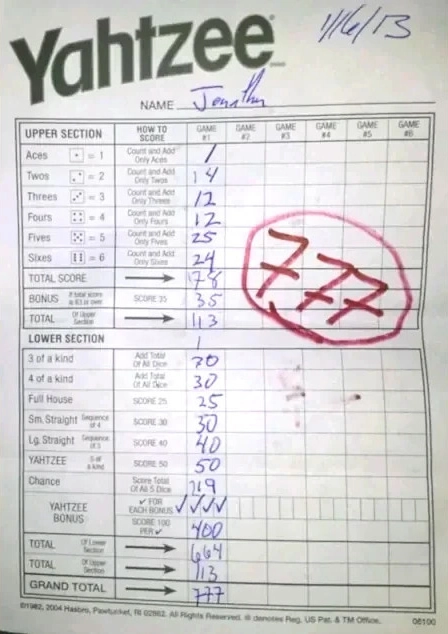
What is the highest score you can get in a single game of Yahtzee? Reaching a four-digit total score is almost unheard of but entirely possible. Consisting of 13 scoring categories, the Yahtzee scorecard allows for the possibility of multiple Bonus Yahtzees and this is the key strategy to maximize points.

What is the highest possible Yahtzee score? The highest Yahtzee score attainable under standard rules is 1575 points: 140 points in the Upper Section, 235 points in the Lower Section, and 1200 Yahtzee Bonus points.

The maximum high score requires rolling a Yahtzee on each turn and using the ensuing Jokers to complete the Lower Section categories. Many of the Yahtzees would need to be in a certain number: the Upper Section's Ones in ones, Twos in twos, etc., and in sixes to max out Three of a Kind, Four of a Kind, and Chance in the Lower Section. If for some reason you are playing without the Bonus Yahtzee rule, then 375 is the high score maximum.

The odds of approaching anything near a 1575 grand total are astronomical. The competent player generally considers a final score in the 250 point range to be a success, and indeed this turns out to be close to the average Yahtzee score using optimization for perfect play. The expected final score of the Optimal Solitaire Yahtzee Player is 254.5896. But like with all Yahtzee odds, this probability is influenced by the player's strategy. Attempting to roll only Yahtzees on every turn yields an average score of only 171.52.

Researchers have devised sophisticated computer simulations that can play Yahtzee at its optimal level. Two of the top strategies that developed as a result are OptExpected and MaxProb.

OptExpected is a computer strategy designed to result in the highest Yahtzee score possible. MaxProb builds on the concept with a scaled-up system that computes the maximum probabilities of achieving a score for all reduced game states. This has resulted a more powerful simulation that is capable to achieving truly high scores.

Millions of their game simulations have been analyzed to determine the odds of achieving a particular result:

Odds of scoring above a particular Grand Total

Grand Total	MaxProb Probability	OptExpected Probability
>150	99.79%	99.13%
>200	91.08%	86.36%
>250	54.19%	48.37%
>300	17.60%	14.31%
>350	9.76%	7.24%
>400	4.93%	3.84%
>450	1.75%	1.14%
>500	1.00%	0.72%

What is a good Yahtzee score? It all depends on the player, of course. But using a powerfully optimzed computer engine you can expect to score 250 points in about half of your games, making it a good benchmark score to measure your progress.

You can play Yahtzee online for free at The Yahtzee Manifesto digitial dice game. Check out the high scores page to see how you stack up to the competition!

High Scores

How Low can You Go?

At the other end of the scoring spectrum, the lowest Yahtzee score ever recorded, or even possible, is a paltry five points. It can be a challenge to roll zeros for all scoring categories but it's impossible to do for Chance. Only a roll of five Ones for Chance allows a player to plumb the lowest depths of the Yahtzee score card.

High Score Records

Many players choose to discard their completed Yahtzee score cards once the action is complete. But in the age of Big Data and monetization of information, this is like throwing away legal tender. More importantly, it puts cherished Yahtzee achievements and milestones at risk of eroding beneath the sands of time.

Players should take pride in their highest Yahtzee score by preserving its legacy for future generations. The simplest method is to keep all used scoresheets in your Yahtzee box or another secure location. When the box is busting at the corners it may be time to relocate the archive to more spacious confines. Even if you haven’t rolled a personal best, develop a system to secure your scorecard documentation. One day you’ll thank yourself.

Before a scorecard with a high score goes into the archive for long-term storage, it deserves a proper celebration. The classic method of sticking it on the refrigerator is always a great way to draw attention to your remarkable feat. Some Yahtzee enthusiasts like to encourage others to add gold stars or other decorations as a sign of their admiration. And to show the utmost respect for Yahtzee accomplishments, consider creating a Hall of Fame to honor the feats of your gaming comrades.

---

 Probability of Rolling a Yahtzee

Dice probabilities are the statistical basis of Yahtzee odds calculation. It follows that a solid understanding of probability theory is one of the keys to mastering the game. Probability theory is the branch of mathematics that deals with the study of random events. In Yahtzee, the random events are the rolls of the dice. The first step in understanding probability theory is to understand the concept of permutations and combinations.

Permutations and combinations are methods for counting the number of ways that a set of objects can be arranged. A permutation is an ordered arrangement of objects, while a combination is an unordered arrangement. In Yahtzee, permutations and combinations are used to calculate the number of ways that a particular dice roll can occur.

For example, when rolling five dice, there are 6^5 (or 7776) possible outcomes. This is because each dice has six possible outcomes (1, 2, 3, 4, 5, or 6) and there are five dice. However, not all outcomes are equally likely. Some outcomes, such as rolling five of a kind (a Yahtzee), are much less likely than others. When calculating outcomes, it’s helpful to use this formula to break down potential dice rolls:

Probability = Number of desired outcomes ÷ Number of possible outcomes

So to get a 4 when rolling a standard Yahtzee die, probability = 1 ÷ 6 = 0.167, or 16.7 percent chance.

Independent probabilities, used to determine the chances when rolling multiple dice, are calculated using:

Probability of both = Probability of outcome one × Probability of outcome two

So to get two 4s when rolling two dice, probability = 1/6 × 1/6 = 1/36 = 1 ÷ 36 = 0.0278, or 2.78 percent.

What are the odds of rolling a Yahtzee?

The probability of rolling a Yahtzee is 4.61%, or about once every 22 turns. Statistics and equations can help us understand Yahtzee on a deeper level but they do not tell the whole story. All Yahtzee statistics based on mathematical probabilities misses one crucial element - the human mind.

A calculation for the probability of rolling a Yahtzee, for example, depends on the player’s strategy, level of risk acceptance, and the current state of the game. Imagine a player on the final turn of the game who is actively trying to roll a Yahtzee and nothing else. They are focused on a singular objective. But the same player in a game’s early rounds may attempt to cultivate a Large Straight and throw away a matching pair, hurting the chances of rolling a subsequent Yahtzee in the process. This more open strategy of playing the dice as they fall results in a lower Yahtzee completion rate when compared to rolling for Yahtzee or bust.

Even computers optimized for perfect play cannot reproduce motivation, intuition, or the multitude of other unique qualities that humans bring to the Yahtzee table. The conditions of the game at hand and the constitution of its players add a layer of complexity that will always affect the pure statistical Yahtzee odds. Human strategy must be considered to calculate the chances of rolling a Yahtzee, or any other scoring combination for that matter.

One of the most useful calculations to measure the probability of rolling a Yahtzee considers a player who is actively attempting to roll Yahtzee with any number. They aren’t locked into shooting for sixes but also have no interest in scoring a Full House. Tim Fulford of Cornell University provides the following probabilities for this scenario using binomial permutations. The binomial distribution is a probability distribution that is used to model the outcomes of a series of independent trials. In Yahtzee, the binomial distribution can be used to model the outcomes of multiple rolls of the dice:

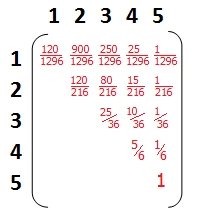
The equations use the following variables:

p = probability of rolling a specific number on one dice (1/6)
q = the probability of not throwing the specific number (1-p) or (5/6)

Rolling five, four, three, two, or one dice gives the following binomial permutations, where the number corresponds to the number of matching dice:

0M, 1M, 2M, 3M, 4M, 5M

So Yahtzee is 5M, four of the same number is 4M, etc.

The mathematical representation of rolling dice looks like this:

Rolling all 5 dice: (p+q)5 = q5 + 5pq4 + 10p2q3 + 10p3q2 + 5p4q + p5
Rolling 4 dice: (p+q)4 = q4 + 4pq3 + 6p2q2 + 4p3q + p4
Rolling 3 dice: (p+q)3 = q3 + 3pq2 + 3p2q + p3
Rolling 2 dice: (p+q)2 = q2 + 2pq + q2
Rolling just 1 dice: (p+q)1 = q + p

1st Roll - One permutation. Roll all five dice and get Yahtzee:

5M = 6p5
or 0.077%

2nd Roll – A few more permutations. Rolled 4, 3, 2, 1 or 0 matching dice on first attempt, then throw a Yahtzee from the remaining dice:

5M = 6p5(1 + 5q + 10q2 + Q + R)
or 1.26%

3rd Roll – Many more permutations to throw a Yahtzee from the remaining dice after two rolls:

5M = 6p5{1+ (5q + 10q2 + Q + R)(1+6Rp) + 5q2 + 10q2[(1+q)2 – 1] + q[(1+q)3 -1] + 5Qp2}
or 4.61%

Using these calculations the chances of rolling a Yahtzee in a given turn are 4.61%, or about once every 22 turns.

But to roll a specific Yahtzee, in sixes for example, the odds tighten to just 1.33%.

Other Scoring Odds

The probability calculation can be quite complicated for Straights and Full House, as it involves various scenarios based on the number of matching sequential numbers that the player has after the first roll. Take, for instance, a Large Straight which, as you know, requires a sequence of five consecutive numbers, such as 1-2-3-4-5 or 2-3-4-5-6.

In the initial roll of a turn, you toss all five dice, leading to 7,776 possible combinations (6^5). Out of these, only 240 are Large Straights. Consequently, the probability of rolling a Large Straight in the first roll is relatively low, approximately 3.09%.

Now, what happens if you don't get a Large Straight in the first roll? Here's where your strategic decisions come into play.

Scenario 1: You have three sequential numbers

For instance, imagine you roll 2, 3, 4, 5, and 6. You'd naturally retain the 2, 3, 4, and roll the remaining two dice. Why? Because you're just one die away from getting a Large Straight, needing either a 1 or a 5. When you roll a die, the chance of getting any specific number is 1/6. Since you need either of two numbers, the probability of achieving your goal in the second roll becomes 1/3 or about 33.33%.

Scenario 2: You have two sequential numbers

Alternatively, let's say your first roll resulted in 2, 3, 6, 6, and 6. Here, you would hold on to the 2 and 3, and re-roll the other three dice. Now you're aiming for either 1, 4, 5 or 4, 5, 6. Calculating the odds becomes more complex because it's dependent on getting a specific combination in three dice. According to computer simulations, the probability of achieving a Large Straight in this situation is approximately 21.53%.

This strategic approach continues into the third roll, where you'd decide which dice to hold based on the second roll's outcome. It is this combination of luck and strategy that makes Yahtzee such an engaging game.

To provide a holistic view, computer simulations that take into account all possible combinations and strategic decisions report the odds of rolling a Large Straight within three rolls to be approximately 32%, or about once every three turns.

Remember, probabilities provide a statistical guideline but not a guarantee of outcome. In games of chance like Yahtzee, understanding these probabilities and odds can inform your strategy, helping you make calculated decisions about which dice to hold or re-roll, thus enhancing your overall gaming experience.

The following graphs illustrates the odds of rolling a particular combination on the first, second, and third roll of a turn. Because of the multitude of variations that exist for each roll, the Full House and Straights cannot be calculated using pure math. This would need to be figured on a case-by-case basis depending on each of the individual player's rolls.

The statistics assume that the player goes for the given scoring category from the first turn and does not deviate in their strategy. Otherwise, it may take longer to achieve a given score as an initial pair may be discarded to roll for something else.

Yahtzee is a dice game that involves rolling five dice and trying to get certain combinations of numbers. The odds and probabilities in Yahtzee depend on the combination you are trying to roll and the number of rolls you have remaining.

In Yahtzee, there are thirteen categories in which players can score points. These categories include things like "Three of a Kind" and "Four of a Kind". Each category has a different probability of being rolled, based on the number of dice and the possible outcomes.

For example, the probability of rolling a Yahtzee (five of a kind) in one roll is 1 in 1296 (or 0.077%).

The odds of rolling a certain combination can also change depending on the number of rolls you have remaining. For example, if you have already rolled a Four of a Kind and are trying to roll a Yahtzee in your last roll, your odds of doing so are much lower than if you had two or three rolls remaining.

Overall, Yahtzee is a game of chance, and the odds and probabilities of rolling certain combinations can vary widely depending on the situation. Players must weigh the risk and reward of going for certain combinations based on the current scores and rolls remaining.

It's important to note that Yahtzee scoring probabilities do not take into account the strategic choices made by the player. Additionally, the odds of rolling a specific combination may change depending on which combinations have already been scored and which are still available to be scored.

---

To calculate useful Yahtzee probability, we must assume that we are dealing with competent players using a sound strategy. Human players, alas, may fall short of this expectation. And their individual playing styles will certainly alter the statistical outcomes. Computers, however, can be programmed to behave logically at all points of a game according to a predetermined strategy. Researchers can use these Yahtzee simulators to analyze millions of games to determine optimal tactics.

Optimal Solitaire Yahtzee Player, by Tom Verhoeff of the University of Eindhoven, was the first model to crack Yahtzee optimization. Its play is optimized to maximize its expected final score, which averages over 254 points per game. The statistical analysis of millions of simulated games offers a deeper insight into dice combination frequency and scoring likelihoods with perfect play Yahtzee:

Yahtzotron

There are a multitude of other Yahtzee simulators but they are only as powerful as their code. Many programs, for example, omit the Bonus Yahtzee entirely as a result of increasingly complex decision-making requirements. Dion Häfner of the Niels Bohr Institute, creator of the Yahtzotron bot, can explain the creative process and inevitable difficulties behind developing a Yahtzee simulator, and the limits of human capacity:

"Achieving perfect play in Yahtzee is challenging (impossible?) for humans because it requires perfectly calibrated probabilities. You will need a flawless mental model to evaluate the risk that is associated with each action. This is hard because it is more quantitative than our intuition can handle."

Yahtzotron is able to average total scores of about 5 to 10 points lower than optimal play. In addition to its precision mode, the program is loaded with pre-trained agents designed to follow certain strategies, such as greedy and play-to-win. It’s a useful tool for analyzing tactical decision making trends and probabilistic outcomes.

ComputerYacht

ComputerYacht is a Yahtzee simulator capable of running millions of games in a short time-frame. It uses a home-brewed algorithm to calculate optimal Yahtzee play. The program’s output records vital data such as the number of games simulated, total score of all those games, minimum and maximum scores, and more. Additionally, the average score is reported – around 267 - as well as the percentage of total games broken down by range – games below 200 points, for instance. Download ComputerYacht for yourself to dig deeper into Yahtzee statistics.

---

 Human Yahtzee Statistics

While computer simulations and optimal play calculators are remarkable tools for acquiring new insights into the game, it is not possible to separate Yahtzee from the human player. Mathematical probabilities will only take you so far.

Studying the tendencies of professional players is a good way to incorporate the human element into your Yahtzee study. Learning from the experts will help you to develop your own Yahtzee strategy and improve your game.

The following statistics were compiled by analyzing the games played during 2010-2020 by the top three players on the Yahtzee Pro Circuit. Categories where the score can vary are represented by the players' average score per game. Those that receive a fixed score reflect the percentage of games in which the category was successfully scored:

Yahtzee Pro Circuit aggregated statistics, 2010-2020

	Louise Proctor	Rick McCallister	Park Hee-Soo
Ones	1.45	1.45	1.63
Twos	5.08	5.08	5.13
Threes	9.08	8.38	8.61
Fours	11.95	11.04	12.28
Fives	15.83	15.94	15.35
Sixes	18.99	18.94	18.83
Upper Section	62.22	60.77	61.78
Three of a Kind	20.36	21.56	19.71
Four of a Kind	12.17	14.15	13.73
Chance	20.22	20.15	19.66
Full House	79.5%	84.0%	93.1%
Small Straight	98.7%	99.0%	99.0%
Large Straight	78.6%	74.0%	77.2%
Yahtzee	42.4%	36.0%	36.6%
Yahtzees per game	0.57	0.46	0.47
Average Grand Total	251.88	244.21	247.15

In the Upper Section, note that all players averaged fewer than three of the target number for Ones and Twos. They each are a low scoring Yahtzee category that are often used as “throw-aways" when a player is unable to record an acceptable score elsewhere on their scorecard, in the hope that they will be able to make up the difference with their Fives or Sixes. Also of interest is that none of the top-three Yahtzee pros were able to maintain an average of 63 total points for the Upper Section, the threshold needed to secure the 35-point bonus.

Advanced Statistics

Yahtzee also makes use of convoluted algorithms to analyze gameplay. One of the most popular is the Full House Dis (FHD), a stat that measures a player’s mastery over the Full House category. Use of a near-optimal strategy will result in successfully scoring the Full House in over 90% of games, prompting many players to deny the Full House until the last possible turn. But the roller must successfully score a Full House in order to have a positive FHD quotient. It increases as Full House opportunities are brushed aside like a common peasant. Thanks to the beauty of the equation, with each dis the FHD quotient rises exponentially:

FH(d²) - f

FH = 1, if you score 25 points for Full House
FH = 0, if you score 0 points for Full House
d = number of Full House disses
f = number of additional Full Houses after scoring a Full House

---

 Learn More about Yahtzee Odds

The standard score odds may be skewed if you play Yahtzee online or in another electronic format. Most computer games, including online Yahtzee and handheld devices, depend on an algorithmic random number generator (RNG). This solution creates the illusion of randomness but is not quite all the way there. A true RNG is the dream of cryptography experts as it could be used to create an unbreakable code. It turns out it’s rather hard to outperform the original random number generator – dice.

Read more about odds, probabilities, and strategy on The Yahtzee Blog:

Yahtzee Variant Games - When playing one of the many variant games like Jackpot Yahtzee or Showdown Yahtzee, the standard probabilities are turned on their head. Decades after their rise and fall, these Yahtzee derivative games still drive us to beat the odds.

Yahtzee House Rules - Experimentation with the official Yahtzee instruction booklet can lead to new and exotic regulations to enact at your home table. House Rules are a great way to provide your gaming guests with a personalized approach to the game. A special rule(s) that applies to games played at a specific location. House Rules are at the discretion of the game host and can be used to modify standard Yahtzee odds.

Yahtzee Strategy: The Joker's Gambit - Put probability on its proper pedestal by pooh-poohing the Yahtzee. A player's level of risk tolerance is tested when passing on 50 points in the Joker's Gambit.

How to Develop a Winning Yahtzee Mentality - Odds and probability are unmoving mathematical constants, right? Not quite. With a winning Yahtzee mentality, you can nudge the odds in your favor. Learn how to get your mind right, then watch your high scores skyrocket.

Yahtzee Odds Calculator

No matter how much you covet that Large Straight, Yahtzee will always be better. More points, more prestige, and it sets the stage for the highest Yahtzee score of your life. It will move your average Yahtzee score in the right direction. But sometimes the decision isn’t so simple. For the times when a tricky roll leaves you grasping at straws, consider consulting a dice probability calculator to work out all the angles.

Use the Yahtzee calculator tool to figure the odds for a given set of playing conditions. A dice probability calculator can help put you on the road to success. A careful comparison of the probabilities will allow you to refine your Yahtzee strategy in exciting new ways. Because just like in life, we’re constantly striving for the highest possible score in Yahtzee. Modern mathematical technology like a dice roll probability calculator is an essential tool for any Yahtzee disciple.

Dice Probability Calculator

---

 Yahtzee Research

Using the latest mathematical techniques, researchers at the World Yahtzee Institute and their colleagues around the globe continue to push the limits of Yahtzee probability and score odds.

In a recent WYI study, Yahtzee was put under the microscope to understand its impact on human cognition and decision-making. The study was conducted over the course of several months with a sample size of 1000 participants, ranging from novice to expert players. The researchers found that playing Yahtzee on a regular basis can significantly improve one's problem-solving skills, strategic thinking, and ability to make calculated risks. The participants who played Yahtzee regularly showed marked improvement in these areas compared to those who did not play the game.

Furthermore, the study also found that playing Yahtzee can lead to an increase in brain activity and stimulation, particularly in the areas responsible for decision-making and critical thinking. This supports previous research that has shown that playing games can have a positive impact on mental health and overall cognitive function. Yahtzee is not just a fun and entertaining game, but it also has significant benefits for brain development and cognitive function. The research team hopes that this study will encourage more people to play Yahtzee and other games that challenge the mind and stimulate cognitive growth.

The following papers constitute some of the world’s most groundbreaking research into Yahtzee theory and strategy:

• Reinforcement Learning for Solving Yahtzee
  Minhyung Kang & Luca Schroeder, Stanford University, 2018
  The researchers present a computer Yahtzee model using a reinforcement learning approach to the game. Their hierarchical learning agent was able to achieve a 99% win rate against a random agent and 68% win rate against a greedy model.

• Optimal Yahtzee: A Comparison between Different Algorithms for Playing Yahtzee
  Daniel Jendeberg & Louise Wiksten, KTH Royal Institute of Technology, 2015
  The game of Yahtzee is a strategic luck based game, which means it should be possible to maximize the total score with an optimal strategy. The main purpose of the study is to compare the results of the optimal algorithm with other useable strategies when playing Yahtzee.

• The three-dimensional dynamics of the die throw
  M. Kapitaniak, J. Strzalko, . Grabski, and T. Kapitaniak, University of Aberdeen, 2012
  A three-dimensional model of a die throw which considers the die bounces with dissipation on the fixed and oscillating table has been formulated. It allows simulations of the trajectories for dice with different shapes. Numerical results have been compared with the experimental observation using high speed camera. It is shown that for the realistic values of the initial energy the probabilities of the die landing on the face which is the lowest one at the beginning is larger than the probabilities of landing on any other face.

• A Nearly Optimal Computer Player in Multi-player Yahtzee
  Jakub Pawlewicz, Institute of Informatics, Warsaw University, 2010
  In case of single player Yahtzee, optimal computer strategies both for maximizing the expected average Yahtzee score and for maximizing the probability of beating a particular score are already known. However, when it comes to the multi-player version, those approaches are far too resource intensive and thus are not able to develop an optimal strategy given current hardware. This paper presents the first in-depth analysis of the multi-player version of Yahtzee.

• The Mathematical Analysis of Games, Focusing on Variance
  Tom Verhoeff, Eindhoven University of Technology, 2009
  Many real-life situations resemble game playing, in the sense that both involve the need for making good decisions in the presence of constraints and uncertainty. It is not surprising that the same mathematical techniques are helpful in both situations. Combinatorial games have seen much progress recently due to improved algorithms and computer hardware.

• An Optimal Strategy for Yahtzee
  James Glenn, Loyola College, 2006
  Solitaire Yahtzee is a complicated game in that the best strategy is not obvious, as it is for simple games like tic-tac-toe, however, it is not so complicated that computing the optimal strategy is infeasible. This report describes the elementary combinatoric and graph theoretic techniques used to compute the optimal strategy for Yahtzee. Once the strategy has been computed, the same techniques can be used to perform statistical analysis of it and other non-optimal strategies.

• Reward Variance in Markov Chains: A Calculational Approach
  Tom Verhoeff, Eindhoven University of Technology, 2004
  Markov chains are not only useful for analyzing puzzles and games of chance, but also play a prominent role in economics and engineering. Attention is often focused on the expected reward (or cost). However, in practice, the variance is also important, because it relates to risk and buffer capacity needed for handling the swings around the expected value. This paper used Markov chains to analyze Yahtzee.

• How to Beat High Scores in Yahtzee
  C.J.F. Cremers, Eindhoven University of Technology, 2002
  The highest Yahtzee score is within reach using an optimized strategy. Learn how to increase the odds of rolling a Yahtzee. Roll a Large Straight, Yahtzee, or Full House with ease. This report builds on prior research to determine a collection of optimal strategies for Yahtzee. To improve your strategy, best practice calls for games of Yahtzee online with a training model.